– This polynomial is known as a cubic spline function – It is very special since the coefficients are chosen to give a. 'linear' - linear interpolation 'spline. Proving that linear programming can be solved in polynomial time. Then learn more about it (read papers, books, etc) and nd out what numerical algorithms are important. Examples: Linear solvers for projection methods in uid dynamics. Eigenvalue solvers for the google matrix. Spline interpolation or approximation of surfaces.

• Polynomial Interpolation Examples

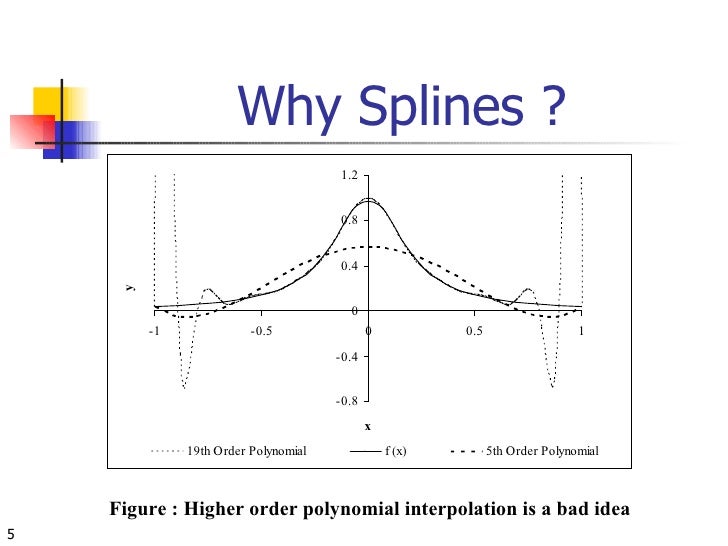
Single knots at 1/3 and 2/3 establish a spline of three cubic polynomials meeting with C 2 continuity. Triple knots at both ends of the interval ensure that the curve interpolates the end points In, a spline is a defined. In problems, is often preferred to because it yields similar results, even when using low degree polynomials, while avoiding for higher degrees. In the subfields of and, the term spline more frequently refers to a piecewise polynomial.

Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through and interactive curve design. The term spline comes from the flexible devices used by shipbuilders and to draw smooth shapes. Contents. Introduction The term 'spline' is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The data may be either one-dimensional or multi-dimensional. Spline functions for interpolation are normally determined as the minimizers of suitable measures of roughness (for example integral squared curvature) subject to the interpolation constraints.

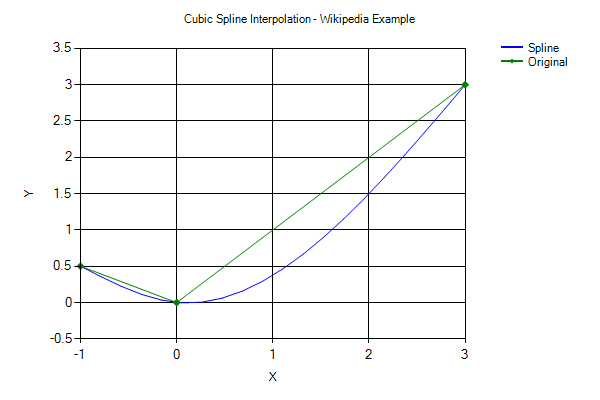
May be viewed as generalizations of interpolation splines where the functions are determined to minimize a weighted combination of the average squared approximation error over observed data and the roughness measure. For a number of meaningful definitions of the roughness measure, the spline functions are found to be finite dimensional in nature, which is the primary reason for their utility in computations and representation. For the rest of this section, we focus entirely on one-dimensional, polynomial splines and use the term 'spline' in this restricted sense. Definition. A wooden spline It is commonly accepted that the first mathematical reference to splines is the 1946 paper by, which is probably the first place that the word 'spline' is used in connection with smooth, piecewise polynomial approximation. However, the ideas have their roots in the aircraft and shipbuilding industries. In the foreword to (Bartels et al., 1987), describes ', a technique used in the British aircraft industry during to construct templates for airplanes by passing thin wooden strips (called ') through points laid out on the floor of a large design loft, a technique borrowed from ship-hull design.

For years the practice of ship design had employed models to design in the small. The successful design was then plotted on graph paper and the key points of the plot were re-plotted on larger graph paper to full size. The thin wooden strips provided an interpolation of the key points into smooth curves. The strips would be held in place at discrete points (called 'ducks' by Forrest; Schoenberg used 'dogs' or 'rats') and between these points would assume shapes of minimum strain energy. According to Forrest, one possible impetus for a mathematical model for this process was the potential loss of the critical design components for an entire aircraft should the loft be hit by an enemy bomb.

This gave rise to 'conic lofting', which used conic sections to model the position of the curve between the ducks. Conic lofting was replaced by what we would call splines in the early 1960s based on work by at and (somewhat later). The word 'spline' was originally an dialect word. The use of splines for modeling automobile bodies seems to have several independent beginnings. Credit is claimed on behalf of at, at, and, and at (see Birkhoff and de Boor, 1965), all for work occurring in the very early 1960s or late 1950s.

At least one of de Casteljau's papers was published, but not widely, in 1959. De Boor's work at resulted in a number of papers being published in the early 1960s, including some of the fundamental work on. Work was also being done at Pratt & Whitney Aircraft, where two of the authors of (Ahlberg et al., 1967)—the first book-length treatment of splines—were employed, and the, by Feodor Theilheimer.

The work at is detailed nicely in (Birkhoff, 1990) and (Young, 1997). Davis (1997) summarizes some of this material. References. Schoenberg, Isaac J. Quarterly of Applied Mathematics. 4 (2): 45—99.

Schoenberg, Isaac J. Quarterly of Applied Mathematics.

4 (2): 112—141. Ferguson, James C. 'Multivariable Curve Interpolation'. 11 (2): 221–228.

Ahlberg, J. Harold; Nielson, Edwin N.; Walsh, Joseph L. The Theory of Splines and Their Applications. New York: Academic Press. Birkhoff (1990).

'Fluid dynamics, reactor computations, and surface representation'. In Nash, Steve. A History of Scientific Computation. Reading: Addison-Wesley. Bartels, Richard H.; Beatty, Brian A.; Barsky, John C. An Introduction to Splines for Use in Computer Graphics and Geometric Modeling. San Mateo: Morgan Kaufmann.

Birkhoff; de Boor (1965). 'Piecewise polynomial interpolation and approximation'. In Garabedian, H. General Motors Symposium of 1964. New York and Amsterdam: Elsevier. Davis (1997).

Epperson (1998). Stoer; Bulirsch. Introduction to Numerical Analysis.

Schoenberg (1946). 'Contributions to the problem of approximation of equidistant data by analytic functions'. Diskdigger pro apk download. 4: 45–99 and 112–141.

Polynomial Interpolation Examples

Young (1997). 'Garrett Birkhoff and applied mathematics'. Notices of the AMS. 44 (11): 1446–1449. Chapra; Canale (2006). Numerical Methods for Engineers (5th ed.).

Boston: McGraw-Hill.